Difference between revisions of "Unanswered Questions"
(this page needs some work) |
m (avoid redir) |
||
| Line 375: | Line 375: | ||
'''Question:''' If he knew the Ceremony was bad and that she shouldn't be doing it, why did he let her prepare for it? Why didn't he put a stop to it all sooner? Why did he keep giving her [[Bree's injections|EPOGEN]]? Why didn't he tell Bree about his concerns either before things got out of control, or the day he was shot? Why didn't he tell her how to lower her ribozyme levels without his help? | '''Question:''' If he knew the Ceremony was bad and that she shouldn't be doing it, why did he let her prepare for it? Why didn't he put a stop to it all sooner? Why did he keep giving her [[Bree's injections|EPOGEN]]? Why didn't he tell Bree about his concerns either before things got out of control, or the day he was shot? Why didn't he tell her how to lower her ribozyme levels without his help? | ||
| − | '''Answer:''' These questions have never been discussed within the show, however there has been debate between fans on this part of the story. Because of the environment that Bree's father was in, he would not inform Bree in case of ruining his cover. Bree was raised in a very loyal Hymn of One home. The possibility for Bree's father's cover to been blown away was very real with his wife being a leading member of the society. If Bree's father attempted any type of blocking [[ | + | '''Answer:''' These questions have never been discussed within the show, however there has been debate between fans on this part of the story. Because of the environment that Bree's father was in, he would not inform Bree in case of ruining his cover. Bree was raised in a very loyal Hymn of One home. The possibility for Bree's father's cover to been blown away was very real with his wife being a leading member of the society. If Bree's father attempted any type of blocking [[the Ceremony]], the [[Hymn of One]] could potentially become suspicious. Also, it has become very apparent since [[The Unthinkable Happened]] video, that her father didn't feel that she was emotionally capable of handling the information he knew about the Order. As time progressed however, it became more and more crucial that she know so she could expose it to the world. As for the EPOGEN, the general belief was that her father was no giving Bree EPOGEN at all, but giving her the serum that Dr. Isaac Gilman created for her to make her trait negative. Or possibly, tested different forms of serums. Is it possible that the EPOGEN, was supposed to enhance the trait positive? Remember though, none of this information has in fact been fully confirmed. So it is still very much debatable. |
{{fakeheader|3|Question 5}} | {{fakeheader|3|Question 5}} | ||
Revision as of 00:27, 20 July 2008

|
This article or section needs to be updated Please update the article to reflect recent events, and remove this template when finished.
|
Since the suspense of Lonelygirl15 is built around a mystery, it is only natural there are many unanswered questions in the plot. This page tries to keep track of them and offers possible answers.
Contents
- 1 Bree
- 2 Daniel
- 3 Cassie
- 4 Gemma
- 5 Jonas
- 6 Lucy
- 7 Watchers
- 8 Deacons and Elders
- 9 Alex
- 10 Nikki Bower
- 11 Jules
- 12 Sarah
- 13 Isaac and Spencer Gilman
- 14 Bree's Parents: Drew and Elizabeth Avery
- 15 Jonas's Parents
- 16 Other Parents
- 17 Order/Hymn of One
- 18 The Resistance
- 19 The Ceremony
- 20 The Party
- 21 Capture in Vegas
- 22 The Box
- 23 Hymn of One Videos
- 24 Back Story
- 25 Random
- 26 See also
Bree
Question: What is the significance of the scar on Bree's back, that was purposely shown in the Swimming! video? Is that the "mark" that the Hymn of One refers to?
Answer: None as of yet. However, the "mark" that the Hymn of One refers to was created by a fan on the MySpace page. The Creators have yet to confirm that they kept it on for a reason.
Question: What happened to Bree while she was with the Hymn of One? What made her all "Hymn-of-One-ish?" Why is her memory mixed up so badly? What is up with Bree's behavior after she was taken back to the rented cabin? Why did she make the video I hAtE tHeSe PeOpLe? If she was being all crazy and spazzed out, how did she edit the video together? Why did she go into a zombie-trance thing in Bedside Manner? Why did she start responding to Jonas? Did she have a plan for escape the whole time, or did it come to her later on?
Answer: Bree was planning to do the Ceremony all along. She was completely aware that her behavior was that of a lunatic or someone in a trance.
Question: Why did Bree escape? Did she really want to go back to the Hymn of One, or was she forced?
Answer: Refer to Answer to Question 2.
Daniel
Question: What did Daniel talk about when Jonas hypnotized him? Did he really talk about Thursday night, or something else?
Answer: It is assumed that Jonas and Daniel were more so goofing off with that response, but it is possible that Jonas really does have hypnotic skills.
Question: Is there any particular reason why Daniel doesn't like to go swimming?
Hole: While this was rumored, and discussed for a while, in Swimming! he did in fact go swimming. At one point in the video, you see Daniel soaking wet. To enforce the idea that Daniel swam, Bree can be heard saying "Daniel got in the water."
Question: In Confrontation, Alex clearly didn't know how Daniel got in the house. How did he get in unnoticed, and what was he doing?
Answer: It has been known that Daniel has a skill for breaking and entering, as seen in Breaking And Entering, Following The Helper and many more videos. He obviously broke into Alex's vacation house, for the sole reason to confront Alex. However, did Bree know that this was the plan? We are unsure.
Cassie
Question: Who is Cassie?
Answer: Within the story, the answer was never really clear. We understood that she moved away, and Bree was not allowed to talk to her after some prank phone calls that they made. From the Creators's end of things, we find out that Cassie was actually Bree's original name. In the original story that inspired the creation of Bree, Mesh Flinders created the central character with the name of Cassie, later on replacing her name for Bree for this series.
Question: Why does Bree randomly remember her and bring her up?
Answer: With the way Bree talks about her, people have reasoned that Bree felt close to Cassie. She was able to relate to her. Bree also felt like Cassie was her connection to the outside world.
Question: Why does Daniel not remember her?
Answer: A theory that is debated is that Daniel does remember her, but is not telling Bree, Jonas, Sarah, Taylor, or Spencer just to keep himself safe from the Order, as Cassie was either a hostage of the Order or a member. Another story is that Daniel was involved in a fight against the Order with Cassie, the Order kidnapped him, and he was brainwashed to never remember Cassie again.
Question: Why was everyone so mean to her?
Answer: None as of yet. Perhaps she was just a lonely goth. Maybe she was a bookworm like Bree, and only had friends such as Daniel. Or maybe she was just known to the entire student body as "that freaky cult girl." She was most probably viewed as the outcast.
Question: What freaked her out about Bree's religion (since up until recently Bree didn't talk about it much, which we know because Daniel didn't really know anything about it)?
Answer: None as of yet. It is a debated theory that Cassie was on the run from the Order just like Bree and Daniel. But, because of the lack of information given about Cassie, we can not know.
Question: Why does Daniel bring Cassie up in the video Miss Me?
Answer: Fans believe this was just a shout-out to the fan spin-off series Cassieiswatching. The video itself followed in Cassieiswatching's editing footpaths.
Question: Is she actually connected to the Order, or has the Order just used her name because Bree talked about her?
Answer: None as of yet. This is actually one of the biggest Cassie mysteries ever. Some fans believe she was just a normal high school girl. Others believe that she too was on the run from the Order. It is unknown if she even has anything to do with the Order. It is still to this day one of the more debated subjects within the Lonelygirl15 universe.
Gemma
Question: What was Gemma's real objective?
Answer: This was never fully answered in the videos, however the OpAphid game answered it, to a degree. Gemma's original mission was to dispose of "Brother," who was there infiltrating the Order in London through his relationship with Gemma. After that plan "supposedly" succeeded, Gemma was later on moved to California, to which guide Bree back into the hands of the Order. However, because of Gemma's previous experience with death, she felt the odd need to dispose of Bree.
Question: Was she really working for the Order, or was it more complicated?
Answer: Many people feel it was more complicated due to conflicting statements within her videos. However the letters between Brother and Tachyon clearly indicate that Gemma was working within the ranks of the Order since the beginning.
Question: Was she really shot by Brother, or was it a ruse?
Answer: Sources have been mixed on this one. While OpAphid and Brother seem confident that Gemma is now in fact dead, Gemma has been mysteriously logging into YouTube and MySpace.
Question: Is Finn, the musician at the party, the same musician that Gemma went on a few dates with?
Answer: This all seemed to be one big rumor or speculation floating around, so let's just leave it at that.
Jonas
Question: Was it just a coincidence that Jonas contacted Bree and offered to help her in her flight form the Order, and then later his parents turned out to be agents of the Resistance? Did Jonas know more than he revealed about his parents' activities?
Answer: Due to present circumstances (as of July 12th, 2007) the Jury seems to vote that this is all purely coincidence. Throughout the series we have learned that the Order has many branches that stem in every direction. So this is very possible.
Question: Was there any significance to what Jonas was mumbling in his sleep when they were chasing down Alex in Missing Days? Could his parents have given him information that he didn't realize was information at the time?
Answer: None as of yet. However most feel that there is little significance. In case it is, Jonas said : "Hm... Buy it! No, I don't try to--" and "Umm... you... it's hot, so turn it off."
Question: When searching for Bree, why did Jonas have a mental break down at a lake?
Answer: The given situation calls for some emotional build up. A break down is bound to happen once in a while.
Question: What is up with Jonas's email to Taylor? Why is it so out of character, and why are there so many mistakes?
Answer: While people argue that it is out of character, we have learned throughout the series that Jonas is a very self conscious and defensive man. So when faced with an attack, he attacks right back. In the email situation, Jonas indeed felt that he was being attacked by Sarah, leading to a emotionally driven attack right back.
Lucy
Question: What is the significance of the map locations on Lucy's computer? Are they locations of eligible Ceremony girls, or of places the Ceremony will be held, or what?
Answer: While this is still out for the Jury, there are many reason debated for these maps. There were five locations mapped, found on Lucy's computer:
Zavalla, Texas
31° 9'30.00?N
94°25'34.00?W
La Crete, Alberta, Canada
58°12'9.10?N
116°25'5.50?W
Wickenburg, Arizona
33°58'7.00?N
112°43'44.00?W
North Topanga Canyon Blvd., Topanga, CA
34° 5'37.00?N
118°36'2.00?W
Adak Island, Alaska.
51°47'46.58?N
176°41'55.98?W
North Topanga Canyon Blvd, Topanga, CA and Zavalla, Texas are both confirmed locations of events within the Breeniverse. North Topanga Canyon Blvd is the location of the Dead Horse Trail, in which the Ceremony was said to take place (both fake and real), and Zavalla, Texas is where they found Jules. It is probable that these are location of candidates for Ceremony girls, as the evidence with Jules shows. However, as Jules was bait to lure Bree into the hands of Hymn of One, it may be just a falsified reason given by the Order.
Question: Why does Lucy seem to show up all of the time, even in Mexico?
Answer: While this one seems to be the magic mystery, we know that Lucy is Bree's "Helper." We know that "Helpers" are also like protectors almost. Making sure that Bree does the right thing. Concerning the Hymn of One, the Ceremony is the right thing. If Lucy did not follow Bree, Lucy would not be following her job description as a Helper.
Question: Is there more to her than we know?
Answer: Well, this is a smart ass remark, but we know nothing about her really. So, probably yes.
Question: Why hasn't she been seen since she showed up in Zavalla? Where is she now?
Answer: Obviously this is an old question, because Lucy shows up sporadically in several episodes after. The last occurence was driving an SUV with a shadow in the passenger side, heading for Bree's old house, while TAAG is exiting the area with Gina in tow.
Question: Why is her computer gone from her apartment? Why did she leave behind a map? Wouldn't she have taken it with when she was traveling?
Answer: The Jury is still out on this one (as of July 12th, 2007), however, the general feeling is that the computer and information is gone because she, and the Order, know that Daniel and Nikki Bower have been breaking and entering into her apartment. While the smart thing to do would be to up security, we know that Lucy likes to play mind games with the group. So leaving clues for them wherever she goes is a great way to lead the mice into her trap.
Watchers
Question: What are Watchers, and what side are they on? What is their goal/purpose?
Answer: From what we have so far been told, the Watchers are there to watch and protect Bree. They will not harm her, or touch her, but watch her location and hold down the fort (if you will) until back up arrives.
Question: Why do Watchers (and apparently most Order members) dress the same? Wouldn't their jobs be easier if they weren't as easily recognizable?
Answer: It is a well known fact that Cults use a specified uniform to make everyone feel equal and unified.
Deacons and Elders
Question: Who are the Deacons? Do they think they are really a part of a religion, or do they know that Hymn of One is just a front for the Order?
Answer: Since we know absolutely nothing about them and we haven't been told anything about them really, we can't really say.
Question: What is the relationship between Deacons and Elders?
Answer: There are several people that think that Elders and Deacons are the same thing. But according to Bree, Elders are higher up than the Deacons, who are community-level. Apparently in the Hymn of One, it is an honor just to be in the presence of the Elders.
Alex
Question: Which side is she on -- does she really think she's helping the Resistance, or is she against them?
Answer: While the Jury is still out on this, because of the phone call that Daniel overheard, the feeling is that because she did not know she was being filmed, she is conflicted. This is when people noted that there were great divisions amongst the Order's ranks on free will.
Question: Who was her husband? Why did they divorce?
Answer: With no explanation to the divorce, it has been speculated that Alex's ex-husband is David.
Question: What happened on her 26th birthday that made her give up photography?
Answer: None as of yet
Question: Why did Lucy pick Alex up at the beach in Mexico? Where is she now and what is she doing?
Answer: Once again, no real answer. However, because of a similar circumstance with Bree's father, Drew Avery, we feel that Alex was picked up for betraying the Order.
Question: Why did she up and move? Where did all her stuff go? How come nobody has seen her? Why does the moving sign outside of her house say "JUST KNOCK!"? Why did she disappear at the same time as Lucy?
Answer: The Jury is still out of this one. However, with the threatening aura surrounding Lucy's crew in the Order, the belief is that Lucy has packed up Alex's stuff and disposed of it. Why? Well, people feel that because Alex betrayed the Order, like Drew Avery and Tachyon's family, she met the same fate, thus, leaving her stuff open for the taking. Unlike Tachyon's family, Alex's stuff was not left behind. Maybe the Order learned their lesson with Tachyon's family, noting that people notice when people disappear and leave their stuff behind.
Question: What are the principles that Alex offers to recite on the phone in Lying Bastards? Who was she talking to?
Answer: The feeling is that she was talking to Lucy, as they are so close. However, there is no real way to confirm that (as we could not hear the other end of the call). However, people feel that she was speaking of the general principle of free will that the Order seems to recognize during the Ceremony. Every girl who performs the Ceremony must do so under her own free will. However, in Bree's case, the Order is manipulating her judgment, to make her free will work for their own profit, therefore eliminating the principle behind free will.
Question: When Alex told Bree, "They have another girl," did she mean Jules, herself, or someone else?
Answer: After the emerging of Jules, this caused for a lot of confusion. While all the evidence seemingly pointed to Alex's change of heart, leading the crew to Jules almost seemed like she was in on the whole plan. Some people believe that she may have said that, as that was the original plan to lure Bree into the trap, but she refused to do so. By saying it, she may have believed it would have saved her from the same fate as Bree's father.
Question: Why did Alex go back to the Order and what was the "one step" she had remaining?
Answer: While this is not known, the feeling is that she was forced to go back to the Order.
Question: Who was Alex talking about that she had visited The Perfect Beach with?
Answer: While we are not sure, there is speculation it could have been a boyfriend or her former husband.
Question: Is she really in the fashion business, or does she travel around doing work for the Order with that as a cover?
Answer: None as of yet.
Nikki Bower
Question: What about Nikki B.? Is she canon now, or was that a one-time-deal?
Answer: While the Creators insist that Nikki B. is not canon, she seems to be the fan's liaison between the real world and the Breeniverse.
Question: What was Nikki B. doing undercover with the Hymn of One?
Answer: While this came as a complete shock to everyone, she seemed to be doing what all good investigative reporters do: investigate.
Question: Since Nikki B. was the one that told BDJ that Jules was the new girl, and Jules just seemed to be a trap, is Nikki B. really a member of the Order?
Answer: Because of her most recent video, we know now that she is not a member of the Hymn of One, but she was kicked out as chocolate is not allowed. We also learned that she was just undercover.
Jules
Question: What about Jules? Was she a distraction, bait, or was she really a new Ceremony girl?
Answer: Because Jules really did not seem to know anything about the Ceremony, and because she seemed drone-like when Lucy came, the feeling is that she was just bait to lure Bree in. After Bree was lured in, we also learned that Jules was trait negative. For some reason we just assumed that Bree was trait positive, and onward we went on a mad scientist hunt.
Question: Why does her birth certificate say that she is not adopted? Are her parents actually her biological parents, or is it a cover from the Order so that no one knows she is adopted?
Answer: Because we now know that she is not a candidate for the Ceremony, we can say that she would not have been adopted, definitely. When we discovered that girls were adopted, one crucial statement was misinterpreted by some to say that most girls are adopted, then they select possible candidates. However, this is not the case. The girls that are taken from their birth parents are in fact candidates from the beginning. However, as time progresses, certain females seem more suitable for the Ceremony.
Question: Why did she have the symbol for EPOGEN in her file, and what is "trait negative"? Is she missing one of the traits that Bree mentioned?
Answer: Unfortunately for us, this is not the symbol for EPOGEN. The symbol that was on her file, was the symbol for the company that distributes EPOGEN, which presumably is the Order. Currently (as of July, 12 2007) we are learning more about what these traits really mean. For more information, stay tuned and check out The Bree Solution.
Sarah
Question: Why did Sarah leave home and join the boys?
Answer: The general feeling for this situation is that Sarah simply disliked her home situation. And because she had graduated, she felt that the time was right to leave home.
Question: Why has Sarah fallen for Daniel so quickly? Does she really like him, or is she using him for something?
Answer: From her actions and words in '12 in 12' it would seem Sarah really did like Daniel, but it may still be a rouse for the Order.
Question: Is Sarah really as promiscuous as she claims?
Answer: While this hasn't be discussed, as Taylor has claimed before her sister has that Sarah is "a slut," then it may be safe to assume that she is in fact very promiscuous. However, there is no way to determine whether this is really a cry for attention or an act of the truth.
Question: Why does she make such a huge deal about "fun" in "Everybody Does It ;)?"
Answer: This seemed to be the "Sarah Way" of helping Jonas. In the end, it was actually very mean of her to do.
Isaac and Spencer Gilman
Question: What is the Wyman Foundation?
Answer: While we don't know much, we do know that Isaac Gilman worked for them, and that they seem to be the foundation of the Resistance or a cover for the Resistance, like the Hymn of One is to the Order. However, none of that has been confirmed.
Question: Who is Isaac Gilman? What kind of work did he do with genetics?
Answer: What we do know is Isaac Gilman was a friend of Bree's father. He was trying to come up with a serum to make Bree go from trait positive to negative, so Bree would be protected from doing the Ceremony. And there is a belief that his initials appear on the documents found in Jonas's cabin.
Question: Who is "the Mistress?"
Answer: She seemed to be a lover of Isaac. The idea that people have gotten, is that because she was seen in the party video (thanks to the power of photoshop we have determined that), we feel that she may work with the Order as well, and could have possibly been in a similar situation as Bree's Father (working against the Order from within). This could have been the reason behind hiding her face.
Question: Who is Ted Fuller?
Answer: As described in the blog, Ted Fuller was friends and Sunday Tennis partners with Isaac.
"(Christmas came early in Bev Hills) As many of you know, my Sunday morning doubles partner, Isaac Gilman, was recently honored by the board of the Wyman Foundation for his advances in genetic something-something. BIG WINK! I know Isaac is a brilliant scientist but, to be honest, his achievements at the net are the key to him being at the top of my buddy list! Last Saturday morning, Isaac and I took on Bev Hills' terrible twosome - Jim Goody & Peter Flood. To say that we won would not and could not embrace the defeat 'that we delivered. Best of three sets? 6-2 6-1 (third set just not needed) Nuf said. I toast to you, Isaac! You are a good man and, more importantly, a great tennis partner."
Question: What were the injections Isaac Gilman was giving Bree? Were they to make her 'trait-negative'?
Answer: While we do not know what they were, from the information that we have been given, it appears that they were to make her trait negative.
Question: What caused Isaac Gilman's car to crash? Was he killed by the same people who killed Bree's dad? Is there a connection between the deaths of Bree's dad, Gilman and Gemma (who were all killed the same day)?
Answer: While this is unknown, it has become growingly suspicious as time wears on. The growing theory is that the Order in fact killed Isaac Gilman, to prevent him from getting in their way.
Bree's Parents: Drew and Elizabeth Avery
Question: What did Bree's dad say that made Bree not want to contact her mother? Is there anything that Bree and her father discussed (other than the obvious information about Bree's mom) that we don't know yet?
Answer: While we may never know this, there is a lot of speculation out there. Some think that Bree's mother may be OpAphid, or on the same level as OpAphid.
Question: Why did she get upset that Bree "projected weakness" by crying?
Answer: While, this is completely unknown, and we may never know, the feeling is that the Order is full of very strong women. It is possible that Bree's mother was hoping that Bree could have some day worked with her, or even taken over her spot one day.
Question: Do we really know that Bree's dad is dead?
Answer: While we have never been given straight forward confirmation on this, the feeling is that he is dead.
Question: If he knew the Ceremony was bad and that she shouldn't be doing it, why did he let her prepare for it? Why didn't he put a stop to it all sooner? Why did he keep giving her EPOGEN? Why didn't he tell Bree about his concerns either before things got out of control, or the day he was shot? Why didn't he tell her how to lower her ribozyme levels without his help?
Answer: These questions have never been discussed within the show, however there has been debate between fans on this part of the story. Because of the environment that Bree's father was in, he would not inform Bree in case of ruining his cover. Bree was raised in a very loyal Hymn of One home. The possibility for Bree's father's cover to been blown away was very real with his wife being a leading member of the society. If Bree's father attempted any type of blocking the Ceremony, the Hymn of One could potentially become suspicious. Also, it has become very apparent since The Unthinkable Happened video, that her father didn't feel that she was emotionally capable of handling the information he knew about the Order. As time progressed however, it became more and more crucial that she know so she could expose it to the world. As for the EPOGEN, the general belief was that her father was no giving Bree EPOGEN at all, but giving her the serum that Dr. Isaac Gilman created for her to make her trait negative. Or possibly, tested different forms of serums. Is it possible that the EPOGEN, was supposed to enhance the trait positive? Remember though, none of this information has in fact been fully confirmed. So it is still very much debatable.
Question: What about the fact that they were not her biological parents? Where are her biological parents? Did they give her up willingly, or was she taken? Are her biological parents in Hymn of One? What about her adoptive parents qualified them to raise Bree, and what did her biological parents lack that disqualified them?
Answer: The evidence within early videos have shown us that Bree's biological parents were not in the Hymn of One and that Bree was taken unwillingly. While quotes stated by Bree do elude to this, it is now known that Bree was bought from her biological mother as an infant in Russia. We do know that the home is a "controlled" environment to better the girls chances for the Ceremony. How these "controls" effect the outcome of the girls, we do not know yet.
Question: Why is Bree suddenly happy with her mother again?
Answer: We now know that Bree's final weeks were a ruse by her to trick everyone. She probably pretended to be happy with her mother.
Jonas's Parents
Question: What's going on with the whole plot involving Jonas's parents? Are they really still alive? Where are they, and why have they been gone so long?
Answer: Thanks to LaRezisto, we now know that Jonas's parents are alive and in the Hymn of One, do not remember Jonas, and have a young teen or preteen daughter Emma. See A Family Affair.
Question: What is the "whacked-out, crazy stuff" that Alex's mom accused Jonas's dad of?
Answer: If you looked back on the Bree videos, you will notice that Bree often found that the activities that Daniel were involved in were "weird." Is it possible that the every day activities of outsiders of the Hymn of One were viewed as "whacked-out, crazy stuff?" You decide.
Question: Was there more to Alex's mom's death than just an accident? What are these pictures that the Order had, proving that Jonas's dad was involved with her death?
Answer: None as of yet. However, because of the nature of the situation between Jonas's father and her, and the situation that seemed to surround the trio, growing suspicions say that the Order may have done away with her. If this is in fact the case, is it possible that Alex knows this, or is the Order leading her on as well?
Other Parents
Question: Why was Alex's mom afraid of planes (in "Apology Accepted?" we find out she said that "planes don't fly, they crash.")?
Answer: None as of yet. This may just be a personality trait to make her seem more human to the fans.
Question: What's wrong between Taylor and Sarah's parents? What was in the message that their dad left that made their mom so sad?
Answer: Taylors mom and dad seemingly are in a midlife crisis divorce. Meaning one parent leaves for a much younger and gravity praising partner, while the other one is left in the dust. As time progresses, the one left standing in the dust, become to follow the same pursuit, as a form of revenge, and in turn finds a more attractive younger suitor. When there are children involved, this usually ends up hurting the children, usually leaving them enraged and vengeful.
Order/Hymn of One
Question: What is the difference (if any) between the Order and the Hymn of One?
Answer: While there doesn't seem to be a clear distinction between the two, what we have been told is that the Hymn of One is in fact a cover up for the Order, allowing them to do what they feel they need to do.
Question: What is the connection between the Order and ancient Egypt? Is there any reason beyond some way to lend credibility to Hymn of One?
Answer: The Egyptian mysticism seems to be just one of the seemingly thousands of religions that the Hymn of One has pulled influences from.
Question: Why are there conflicting ideas about capturing Bree within the Order?
Answer: While this is being debated still to this day, the general feeling is that there seems to be much division within the Order and The Hymn of One with Bree. While some see it as it must be done completely under her own free will, others feel they can manipulate her free will for their own profit and others feel that they can simply force her to do the Ceremony. This feeling came about during the Alex days. We really began to notice that, even within the Order, people were choosing sides.
Question: What is the significance of all of the "free will" talk in the Order? Is it just something that the Hymn of One uses to get people in, or is it really part of the Order's objectives, or what?
Answer: While we are not sure, it is known that many religions focus a lot on free will. We also know that many cults use free will, and manipulation of free will to obtain and comfort their members.
Question: What is the "eternal song"? Is it literally a song, or just a metaphor of some kind?
Answer: Due to the information provided at the seminar and through the videos, the feeling that we have been giving is that it is more of a metaphor, but can be taken on a literal sense as well. The feeling that we have been given is that for every person, there seems to be a different eternal song. However, this has not been fully confirmed.
Question: Why did the Hymn of One ask what it did on the "audition" survey? What were the significances of the various answers?
Answer: While there is no definite answer on this, this seemed to be to determine the personality qualities and how they would fit into their belief system, or how they could help you become more like them.
Question: What is with the mantra "The Hymn of One is fun?"
Answer: This seems to be just a mantra to lure followers into the Cult. Many Cults use these type of mantra's to lure people under their own "free will," along with treats such as spin art and pizza.
The Resistance
Question: What is in "the Order of the Modern Empire" other than the Theta/Pi symbol and list of initials?
Answer: the Order of the Modern Empire is what seems to be a brief run down of the History of the Order, the Objectives, the Projects and important members and their history. While we haven't gotten a direct copy of what it is, Daniel and Jonas did let us know that is is a very well put together document outlining the Modern Day history. As for the OpAphid release of information, it has been suspected that there may be some crucial evidence on a certain page, as on the bottom of the OpAphid page, there was a page number. However, that has yet to be confirmed as well.
Question: Is there still a resistance group alive (besides our trio, of course)?
Answer: While we are almost lead to believe that Isaac Gilman and Drew Avery were the last of the Resistance, because of the early Hymn of One videos and the messages contained in them, it may be safe to assume that there are in fact more members of the Resistance within the ranks of the Order.
Question: Besides physical training, did Bree learn anything from Tachyon during her recent stay with her?
Answer: While we don't know, it seemed that Bree may have learned a bit about maturity and how to handle herself in certain situations.
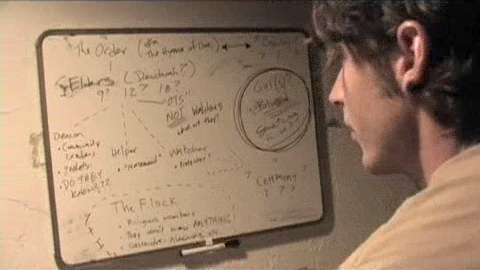
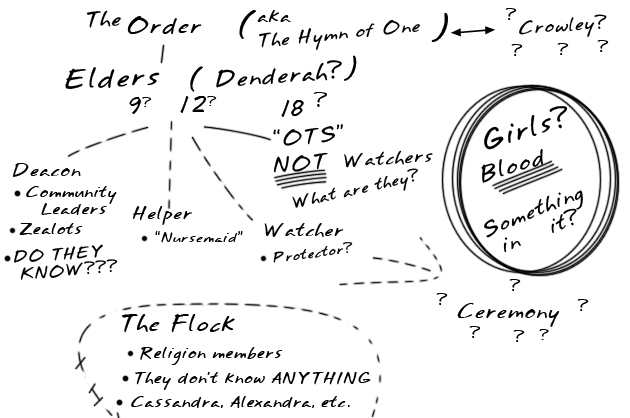
Question: What does the stuff on the whiteboard in the bunker mean? What did they change it to say?
Answer: Here is a photograph of the Whiteboard when we first saw it.
What we have figured it to say is Under Elders (Denderah?):
- 9? 12? 18?
- Deacon. Community leaders. Zealots. DO THEY KNOW???
- Helper. "Nursemaid"
- The Flock. Religion members. They don't know ANYTHING (then something I can't read)
- Watcher. Protector?
- "OTS" NOT Watchers. What are they?
- (Within the circle) Girl(s)? Blood, Something in it?
- Under the circle, the word Ceremony? appears, also surrounded by question marks
Here is the Recreation of the whiteboard:
While in a video shortly after showed changes in the whiteboard, I have yet to find the pictures of the changes
Question: What else did they find in the bunker? Was there anything to find?
Answer: It was discussed slightly that they had found the bare essentials for research and living in the bunker. However no information about documents or materials that could help the fight against the Order was discussed other then the white board.
The Ceremony
Question: In "Order of Denderah", it is implied that the Ceremony takes place in mid-October- is this the only time it takes place?
Answer: Bree's Ceremony took place on August 3rd.
Question: What is the Ceremony, anyway? Why is it so important that it be done, especially since Hymn of One isn't even a real religion? Or is it a real religion that the Order takes advantage of?
Answer: While we haven't gotten a full explination of what the Ceremony is, we do have some interesting information to go on. So far we have learned that the Ceremony involves blood, and possibly a loss of a large amount of blood. The evidence that points to this are Bree's injections being EPOGEN and her diet containing lots of Iron filled foods such as red meats. We also know that the Ceremony must have more to do with Blood and possible regeneration due to the information given to us through the RNA clues and hints. The Ceremony kills the girl involved, presumably through blood loss. Steve of the KateModern series suggested that the Elders use the Ceremony girls' blood for eternal life.
Question: What were the exercises that Bree and Jules talked about? What is the selection process for girls to be chosen for the Ceremony? Why Bree and Jules (if, of course, Jules was actually a Ceremony girl)?
Solutions While Bree still hasn't told us what these exercises were, due to recent events, we may be able to assume that these exercises are to help induce better circulation.
Question: What is different about them than the other girls placed in "controlled environments?"
Answer: We are still figuring this one out! Stay Tuned! (July 12, 2007)
Question: What specific aspect of the Ceremony requires use of EPOGEN?
Answer: While we aren't 100% sure, and nothing has been confirmed, this may be a method used by the Order to enhance her trait, or enforce her trait.
Question: What special diet was Bree on, and why (we know she said it involves a lot of red meat and avoiding sugar, but what else does it entail, and why)? If Jules isn't a Ceremony girl, why was she doing exercises and on a special diet?
Answer: Well, for one thing, if Jules wasn't a Ceremony girl, and was just bait, everything she said may not be that creditable. So she may have no been doing exercises and she may not have been on a diet, but just told us that to bait Bree in. As for the information Bree gave us, it would appear that at least one aspect of her diet was that it was high in iron (she was also put on iron supplement pills). Iron is essential to red blood cells. However, very high levels of iron intake can be toxic.
Question: What exactly is the "purity bond" and why is it crucial?
Answer: While this is still under much debate, people wonder if the purity bond was ever really that crucial. People are now wondering if it was actually more of a cover and a ploy to make it seem more creditable as an actual religious Ceremony other then something else. The bond seemed to govern Bree's interactions with the opposite sex, and was thus speculated to be something along the lines of an abstinence pledge. This may be required of ceremony girls to ensure that they do not contract sexually transmitted diseases that could be transmitted to the Elders who receive their blood.
Question: What was Bree's dad giving her that could lower her ribozyme levels?
Answer: As we are still learning about the serum, we do not really know yet. So stay tuned!
Question: If women are so important to the Order, couldn't they just use trait positive boys for the ceremony?
Answer: None as of yet, but perhaps males cannot be 'trait positive'.
The Party
Question: At the party in the "Uncle Dan" videos, why do they very obviously point out the musician guy?
Answer: The musician guy seemed to be the rudest one at the party, so that could have simply been the answer to this question. However some people speculate that this is the musician that Gemma dated. Or it could just simply be a more obvious way to enforce to us fans that Daniel is a geek.
Question: Who was the guy arguing with Alex, and why were they arguing?
Answer: While the answer to who he was, was never clearly given, they answer to why they were arguing was clearly given within that video. The guy obviously felt completely uncomfortable by Daniel and Jonas being there. While the majority of the persons at the party seemed to be with the Order, we have assumed that because this was a party concerning Order relations, this may be someone who in fact knows exactly who they are, and what threat they pose to the safety and secrecy of the Order. This could be why he was not comfortable with Jonas and Daniel being there, and he may have even been the informant to Lucy that Alex was in fact feeling for their situation.
Question: Why does Toby struggle to say Beth is a reporter and then Beth cuts him off?
Answer: Some people have questioned this, and have concluded that some of these "back stories" that people have given may have been a cover up. Once Daniel and Jonas walked into the room, they knew they were dealing with outsiders, so they felt the need to be secretive about their purposes there. Some people also believe that this may have been a trap to lure Daniel into speaking about Bree and their situation as to the interesting reaction people gave to Jonas when he began to mention why he was visiting his Aunt. So some people believe that these may have been made up stories to help enhance the trusting mood within the party.
Question: What about the comment about Jonas's "file"?
Answer: While we haven't been confirmed on this, there is speculation that this file that they spoke about what the file that they found at Alex house. Some people also believe that there is information that the Order has recently discovered that they may have missed in their clean up of Jonas's parents lives. Some people have also gone as far as speculating that the Order in fact wants Jonas's money, as they feel it rightfully belongs to them, as supposedly Jonas's parents are members of the Order now.
Question: What did Alex tell Sonia about Jonas? Why would she talk about him if she hasn't seen him in about six years?
Question: Why does Carl flip out when Daniel tries to talk to Sonia and him?
Question: Why was there a picture of Lucy, and who is the other woman? Is the other woman Rebecca? Was she really lying about her connections to the Order and Hymn of One? Why did she invite Daniel in for tea?
}}Solution to The Party }}
The remainder of the questions seem to gear around one simplified answer. The party was a gathering of member of the Hymn of One. Either they were all completely taken aback to see two members of the internationally known Resistance at their party, or this was all stages to lure them into speaking about Bree and leading them to her. While the debate is still wavering along, the clear solution here is that the party was in fact a gather of the Order and the fact that Daniel and Jonas, two people who are publicly known as against the Order, made them completely uncomfortable. They probably thought that Jonas and Daniel knew what was going on, and possibly Alex was in on it. Remember though, none of this has really been confirmed. It's been hinted at, but not directly confirmed yet. While we can probably safely assume this with the appearance of attendees of the party within the Hymn of One videos, we can not 100% say for sure just yet.
Capture in Vegas
Question: Who captured Bree, Daniel and Jonas?
Answer: Alex revealed that the person who captured them in Vegas was a 'Shadow'. The personal bodyguards of the elders.
Question: Who was the interrogator?
Answer: This is assumed to be the same person who kidnapped them, as we were given information indicating that there was only one person involved.
Question: Where were they staying?
Answer: According to Nikki B's investigation, it seemed to be a off-highway motel. While this has not been 100% confirmed as of this date, most people assume this is where they were held captive.
Question: How did they escape?
Answer: Absolutely no information was given yet on how they escaped. What we do know is that all they remember is being captured, then running through the desert. They also remember the Watcher shooting the kidnapper.
Question: Why did a Watcher kill their captor and let them go?
Answer: While we have no confirmation on this, the general feeling is the Watchers are there to watch and protect. If they do this, then they probably call for back up to obtain Bree.
Question: How did they find Jonas's car again?
Answer: While this is unclear, and has not been confirmed, we have assumed that Jonas found his car in the desert after the kidnapper was shot. The motel was probably located close by to the location of shooting, leaving Bree, Daniel and Jonas to walk to their vehicle.
Question: We know Bree was told to do the Ceremony, and Daniel was told to go home, but what exactly was Jonas asked about? When they asked about his parents' death, why did he say "I don't want to play anymore?" Why does the interrogator say "This is no game?" Does Jonas know more about his parents' death than he realizes (maybe it's in his subconscious somewhere)?
Answer: While we don't know, really at this point only time will tell.
The Box
Question: Why did Bree's dad leave a box under a stump?
Answer: It seems that Bree's father left the information under a stump because he wanted Bree to know what was going on exactly. While this hasn't been 100% confirmed, it seemed that Bree held onto the letter because she felt that she could figure it out herself. When she couldn't, obviously it lead to her capture and return to the Hymn of One. When Daniel and Jonas released the letter, it lead us to this stump. It contained information pertaining to Bree's condition and why she is trait Positive. While we have not been able to see 100% what the information is, it is obviously very important to Gilman's research.
Question: What was in the rest of the letter from Bree's dad in the box?
Answer: So far what we do know is that is says the following: "Dear Bree, I'm so happy that you were able to find this box. Right now, you're with Daniel. I'm not sure when I'll be able to see you again, but I want you to know that I have faith that you'll find your way. I've raised you to be the strong and independent person that you are. Follow your heart. Don't let others influence you with promises of inner peace and salvation. We both know that doesn't exist in the world of science. This box holds many more important secrets of the Hymn of One, you, and what lies ahead in your life."
What we don't know is what Daniel says he is not ready to read yet. Why? Well we don't really know. What could it be?
Question: What else was in the notebook with the ribozyme charts?
Answer: Only time will tell. How could we know, if Daniel and Jonas don't ever know?
Question: Was there anything else in the box?
Answer: What was in the box? We know that there was a letter, a notebook filled with information, graphs showing Bree's levels of ribzomes or her special ribzome and a collage that Bree made for her father.
Hymn of One Videos
Question: Why does "Sing With Me" open with a large star in the middle of the screen followed by a smaller shooting star?
Answer: Well as this hasn't been confirmed, we can speculate that astronomy has a large part to do with the teachings of the Hymn of One. As we know, Bree is a big fan and extremely knowledgeable about astronomy. Otherwise, it could have just been a funky eye catching graphic.
Question: Why are Sonia and Carl with Bree?
Answer: As we don't know for sure, we speculate that they are recruiters as they were at the seminar, and these are recruitment videos.
Question: Why is Bree wearing a bandage again? Is she taking EPOGEN again?
Answer: While it hasn't been confirmed, it is believed the Bree will go ahead with the Ceremony. Therefore, the rebuilding of her strength to be able to complete the Ceremony is crucial.
Question: Why is everyone wearing white? Why is Bree wearing jeans, when the other two are wearing either khaki pants?
Answer: While we don't know for sure, what we do know is that within Cults, they often feel the need to strengthen bonds between their sisters and brothers by becoming unified in not only thought, but also appearance. An example of this is Heavens Gate.
Question: Why is there a shot of Boston at the end of each video?
Answer: While we are still debating this, this seems to be just a graphic used. However it may be a new location for the adventure to take place.
Question: How are secret messages ending up in the Hymn of One videos? Who put them there, and why?
Answer: As we found out in Mission Possible Alex is TCC. We found out that Alex was in fact the mole, and who was the person who put the messages into the Hymn of One videos.
Back Story
Question: What is the significance of the girl abducted in 1943 by Crowley (since we know it is an event that never actually happened)?
Answer: While we aren't sure on what the significance really is, we do know it may be important. However, it may have been another oops on the creators researching part, as there are many fictional stories concerning Crowley. Hopefully it will be revealed in the future.
Question: Who is the family that Gemma says disappeared? If she really thought Bree should do the Ceremony, why did she scare her by saying that after the Ceremony, that family disappeared? What happened to them? Did they really exist, or did Gemma (or someone telling her what to say) invent them?
Answer: While we don't know the full story on this family, what we do know is that this is in fact Tachyon's family. We do know that something extreme happened to them, and we also know that Tachyon did not wish to speak of them too often as she did not look at them too fondly. However, once again, we do not know the full story, and may never know now.
Question: What happened between Taylor's parents? Is it significant to the story, or is it just character background?
Answer: While some people feel that there is more to the story, we can only take it for what we have been told. What we have been told is that Taylor and Sarah's father left their mother for a younger woman. It seems to be just character background, but because this is the Breeniverse we can never be too sure.
Random
Question: Why is the tag "hamster" used in quite a few videos that have nothing to do with hamsters?
Answer: This is something we do know. Hamster was used in a tag in the videos as Mesh's often used nickname on his films was Hamster.
Question: What happened with "the Cowboy"? Wasn't he supposed to be central to the plot?
Answer: While this seems to be a writing mistake, people have wondered if this could have been the same kidnapper from Las Vegas.
Question: What is the significance of longitude and meridians? Bree made a whole video about it (and the story she told was a myth, which she treated as fact, which seems to indicate it is an important topic), Jonas talks about his parents being lost at sea at a particular longitude, Jonas says that Alex's mom used to talk about them a lot, then - so what's the big deal? Are meridians referring to geography or Chinese medicine, or something else entirely?
Answer: While we still are out on this one, maps do have a significance to the story.
Question: Does Pluto have any significance in the story, as it has now been mentioned three times in the series?
Answer: While we aren't sure on this one, Pluto seems to just symbolize outcasts. And as Bree often feels like an outcast, this could be her way of expressing that.
Question: Did Bree and Jonas sleep together, or did he just try to make it look that way?
Answer: Daniel confirmed they did during 12in12 by shouting "You slept with her!".